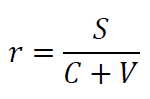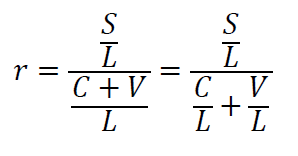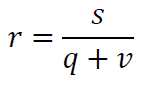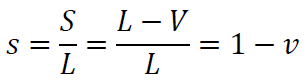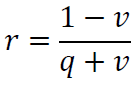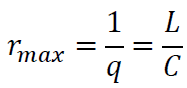…uno di “quelli del lavoro vivo”
Se Marx avesse sviluppato fino in fondo la categoria di “lavoro diretto”, accantonando quella di “lavoro morto” cristallizzato nei mezzi di produzione, vi sarebbe stata un’implicazione di rilievo per la definizione del saggio generale del profitto e delle relative componenti.
Come è noto, il saggio generale del profitto è definito da Marx come:
dove S è la massa totale di plusvalore erogato nella produzione (ipotizzando, per semplicità, un coefficiente di rotazione unitario), C è il nuovo capitale costante impiegato nel processo produttivo e V è il capitale variabile. Sempre per semplicità, possiamo ipotizzare che l’unità di misura nominale sia stata definita in modo tale che l’espressione monetaria del tempo di lavoro sociale necessario sia unitaria, dato il prodotto per unità di lavoro.
Possiamo ora riscrivere l’equazione del saggio generale del profitto dividendo numeratore e denominatore non già per V, come fece Marx, ma per L, dove L=V+S esprime la giornata lavorativa complessiva o lavoro diretto. Si ottiene:
Se chiamiamo v il valore unitario della forza-lavoro, allora l’equazione sopra può essere riscritta come:
dove s è il saggio di sfruttamento, ora ridefinito nell’intervallo [0,1] e q è una variabile più vicina al coefficiente tecnico di Solow che alla composizione organica marxiana.
Infine, è facile verificare che il saggio di sfruttamento non è che il complemento ad uno del valore unitario della forza-lavoro, ossia:
Possiamo, dunque, riscrivere il saggio di profitto come:
da cui si vede che quest’ultimo dipende solo dal valore unitario della forza lavoro v e dal coefficiente tecnico q. In ambedue i casi, si tratta di una funzione decrescente.
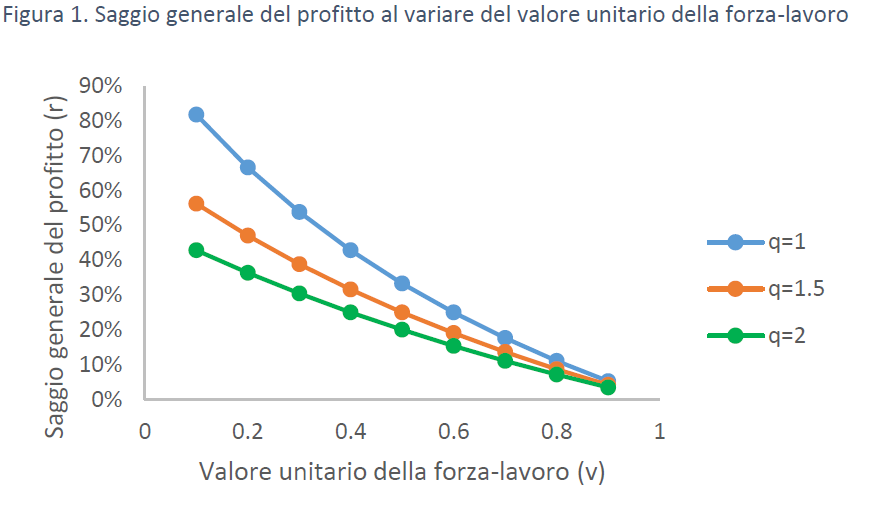
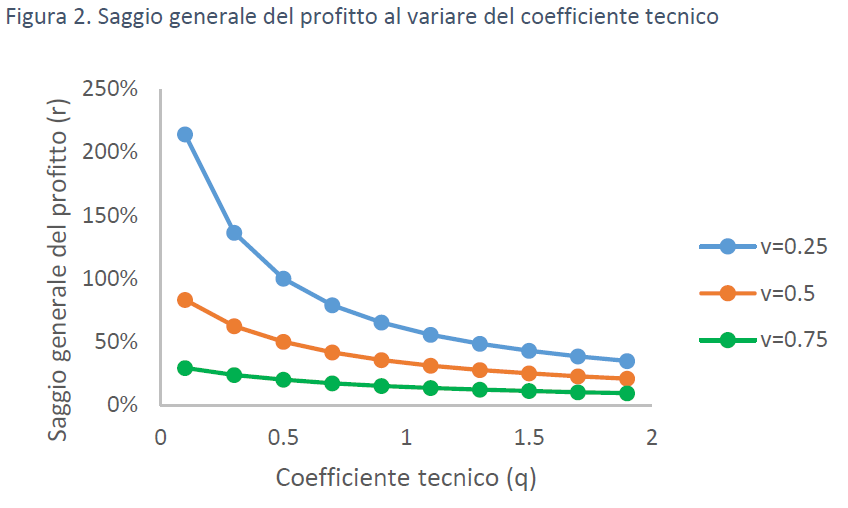
Le figure 1 e 2 mostrano come varia il saggio generale del profitto (r) al variare del valore unitario della forza-lavoro (v) e del coefficiente tecnico (q), rispettivamente, ferma restando l’altra grandezza.
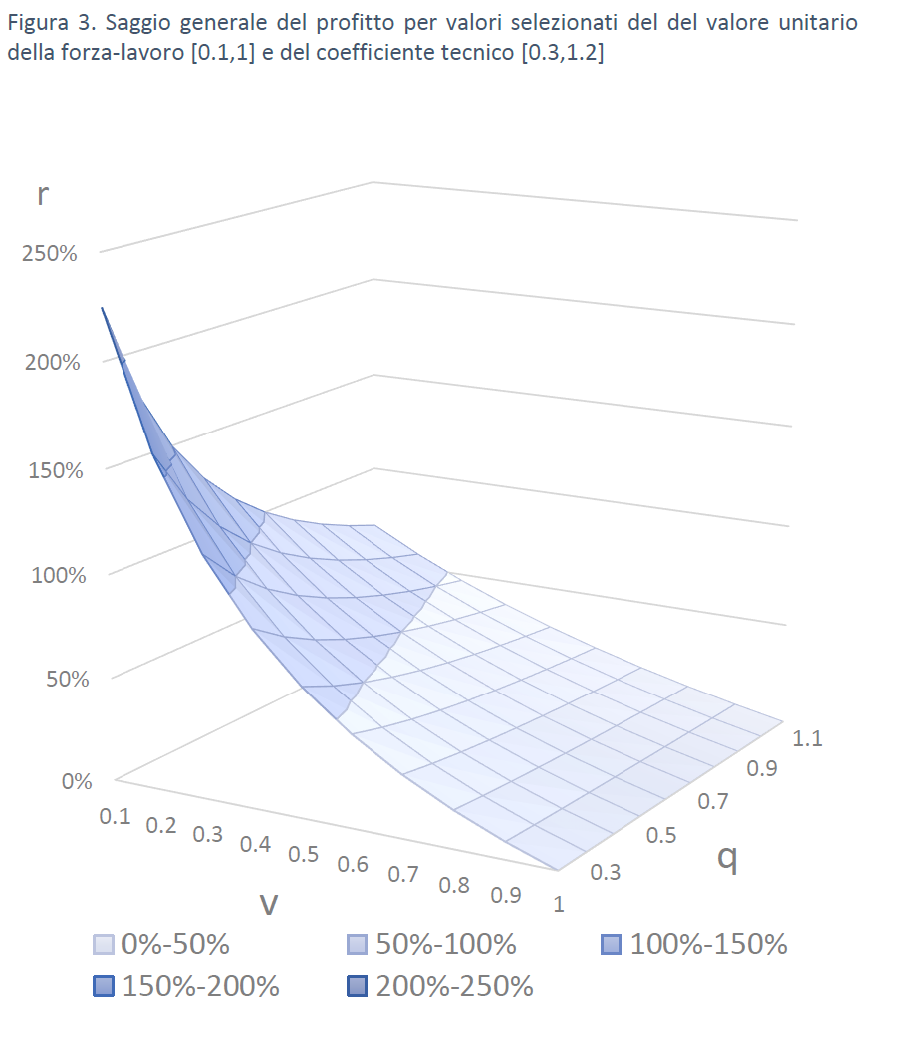
Il saggio generale del profitto cresce al cadere del valore unitario della forza-lavoro (ossia al crescere del saggio di sfruttamento del lavoro) e al ridursi del coefficiente tecnico (ossia al ridursi del valore della dotazione di capitale costante per unità di lavoro impiegata nella produzione). La figura 3 mostra proprio come v e q co-determinino r:
Un’ultima annotazione. Che ne è del saggio massimo del profitto? Quest’ultimo si può calcolare ponendo v=0 (i lavoratori vivono di “sola aria”) nell’equazione del saggio generale del profitto, da cui:
Il saggio massimo del profitto è quindi pari all’inverso del coefficiente tecnico. Naturalmente, il saggio minimo si ha quando v=1 ed è facile verificare che corrisponde a zero.
Perciò, se si accetta, come “fatto stilizzato” ovvero sulla base dell’evidenza empirica, che q tenda a crescere nel tempo allora il saggio massimo del profitto dovrà cadere, imprimendo prima o poi la stessa dinamica anche al tasso effettivo di profitto.